viernes, 5 de octubre de 2018
LA CIRCUNFERENCIA
LA CIRCUNFERENCIA
Es el conjunto de puntos de un plano que están a igual distancia de un punto fijo llamado centro.
La circunferencia constituye la frontera del círculo.
Para trazar una circunferencia se usa el compás.
En una circunferencia se pueden trazar varios elementos: radio, cuerda, diámetro, arco, secante y tangente.
Radio es la distancia que hay del centro a cualquier punto de la circunferencia.
Cuerda es el segmento de recta que une dos puntos de la circunferencia.
Diámetro es toda cuerda que pasa por el centro de la circunferencia. Es dos veces el radio.
Arco: es una porción de la circunferencia.
Secante es la recta que corta a la circunferencia en dos puntos.
Tangente es la recta que toca a la circunferencia en un solo punto.
La circunferencia constituye la frontera del círculo.
Para trazar una circunferencia se usa el compás.
En una circunferencia se pueden trazar varios elementos: radio, cuerda, diámetro, arco, secante y tangente.
Radio es la distancia que hay del centro a cualquier punto de la circunferencia.
Cuerda es el segmento de recta que une dos puntos de la circunferencia.
Diámetro es toda cuerda que pasa por el centro de la circunferencia. Es dos veces el radio.
Arco: es una porción de la circunferencia.
Secante es la recta que corta a la circunferencia en dos puntos.
Tangente es la recta que toca a la circunferencia en un solo punto.
La lúdica en las Matemáticas
El juego y la matemática, en su naturaleza misma, tienen rasgos comunes. Es necesario tener en cuenta esto, al buscar los métodos más adecuados para transmitir a los alumnos el interés y el entusiasmo que las matemáticas pueden generar, y para comenzar a familiarizarlos con los procesos comunes de la actividad matemática.
Un juego comienza con la introducción de una serie de reglas, una determinada cantidad de objetos o piezas, cuya función en el juego está definida por esas reglas, de la misma forma en que se puede proceder en el establecimiento de una teoría matemática por definición implícita.
Edwin Carlos Lévano Chamorro, Magister en educación y especialista asociado de Ediciones Corefo, nos brinda 5 razones por las que es importante aprender matemática de manera recreativa.
1. El aprendizaje a través de la matemática recreativa permite a los estudiantes construir su pensamiento lógico, desarrollar sus capacidades, habilidades y destrezas para enfrentar la vida con satisfacción. Permite además, generar el conflicto cognitivo y reta al estudiante a que busque diversas alternativas de solución a los problemas planteados.
2. Dado que la matemática es necesaria para comprender el mundo desde sus contextos, necesidades y exigencias; operar sobre él requiere del enfoque por resolución de problemas. Este enfoque utiliza diversas estrategias metodológicas para una mejor formación del pensamiento lógico, comprensión y aplicación a la vida diaria. Dentro de las diferentes estrategias de aprendizaje, tenemos el uso de laboratorios y talleres matemáticos, los cuáles, permitirá reforzar los conceptos y teorías aprendidas en el aula de clase.
3. Con la matemática recreativa, los estudiantes aprenden a través de la manipulación y la representación de diversos materiales concretos que se les pone a la mano. La actividad lúdica y el uso de materiales, son una excelente oportunidad para poder aprender de manera motivadora y recreativa, sobretodo porque ayudan a descubrir estrategias para trabajar bajo el enfoque de la resolución de problemas.
4. Hoy en día existen diversos recursos didácticos que la escuela puede brindar, desde los materiales estructurados conocidos, hasta los que se pueden adaptar y poner en práctica, como los dominós, ruletas, bingos, puzzles, ludos, etc.
5. Además, el aprendizaje a través de las matemáticas recreativas, considera las inteligencias múltiples, así como los diversos estilos y ritmos de aprendizaje de los estudiantes, lo que permitirá al docente obtener mejores resultados en el desarrollo de sus clases.
Juego de Bingo
El BINGO
es una gran manera para que los niños se emocionen e interesen en el
aprendizaje de las fracciones.
ADVERTENCIA:
¡Una vez que los niños empiezan a jugar, querrán más y más BINGO!
¡El Bingo
de fracciones equivalentes es siempre un éxito con los alumnos chicos! Es una
gran manera para que los estudiantes refuercen y practique el cálculo de
fracciones equivalentes y el aprendizaje de los conceptos básicos!
- A
cada jugador se le da una tarjeta de bingo con fracciones al azar.
- Se
decide quién será la persona que llama. El llamador es responsable de
llamar a las fracciones del bingo y no es un jugador en el juego. Así que
la persona más probable que sea la persona que llama es el profesor o los
padres.
- La
persona que llama o cantador debe recordar a todos que el espacio central
de las tarjetas, aquel marcado con una estrella, es libre y todos deben
marcarlo.
- La
persona que llama escoge una lista de fracciones preparada que sustituye a
la tómbola en el juego tradicional.
- La
persona que llama lee una fracción a la vez y la tacha, y permite a los
jugadores marcar en una de las visualizaciones de fracción en la tarjeta
si coincide. Los gráficos de las cartillas pueden ser de fracciones
equivalentes (no reducidas) por lo que los jugadores deberán reducirlas
mentalmente si las quieren marcar.
- Si
la fracción llamada, no coincide con ninguna de las representaciónes
gráficas de fracciones en las tarjetas, el jugador no marcará ningúna en
su tarjeta.
- El
juego continúa hasta que alguien tenga marcas a lo largo de de una fila de
su tarjeta, a lo largo de una columna de su tarjeta, o a lo largo de una
diagonal.
- El
primer jugador en marcar uno de estos patrones deben ponerse de pie y
gritar "¡BINGO!"
- Después
de que un jugador se haya declarado ganador, el llamador debe comprobar el
BINGO para asegurarse de que el jugador realmente hay marcado las
respuestas que responden a las operaciones que fueron llamadas. Si todas
sus respuestas se comprueba, habrá felicitaciones.
- Si
usted desea tener más de un ganador, el juego sigue. Esta es una manera de
tener múltiples ganadores. Mientras el primer ganador espera la próxima
partida, los demás siguen jugando.
- Muchos
maestros y padres de familia se dan cuenta del potencial de jugar bingo
para ayudar sus niños a ver que las matemáticas son divertidas e
interesantes. Algunas escuelas ya han comenzado clubes de matemáticas que
compiten contra otras escuelas.
- Así
que si estás buscando actividades de matemáticas divertidas para niños, te
darás cuenta que en un juego de bingo con las matemáticas es una manera
buena y muy barata de hacer trabajar la mente de los niños con las
matemáticas.
- Este
archivo de tarjetas de Bingo imprimibles es perfecto para jugar Bingo de
Fracciones. Contiene 50 tarjetas de BINGO únicas a todo color, dos tablas
en cada hoja A4. Esto permite
- Imprimir
las tarjetas de
Bingo.
- Cortar
las tarjetas dividiendo las hojas en dos.
- Pedir
que cada niñ@ escoja una tarjeta de Bingo.
- Imprimir
las hojas con las
tómbolas de bingo. Consisten en las fracciones reducidas hasta
décimos.
- Seleccionar
la lista/tómbola de fracciones a ir llamando.
- Llama
la fracción. Los niños deben buscarla, y verificar si existe en sus
tarjetas.
- Cuando
el niño tiene la respuesta en su hoja, la tacha con una X o coloca
una ficha sobre la casilla correcta.
- El
primer jugador en tener cinco respuestas correctas es el ganador.
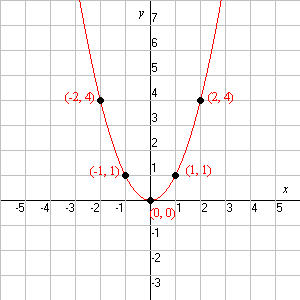
LA PARÁBOLA
Concepto
de Parábola
La parábola es el lugar geométrico de todos los puntos del plano, cuya distancia a un punto fijo es igual a
su distancia a una recta fija. El punto fijo F recibe el nombre de foco de la
parábola y la recta fija directriz de la
parábola.
Principales Elementos de la Parábola
ECUACIONES ORDINARIAS DE LA PARÁBOLA
A continuación un video para que conozcas más acerca de la parábola
Suscribirse a:
Entradas (Atom)